Wave Painter#
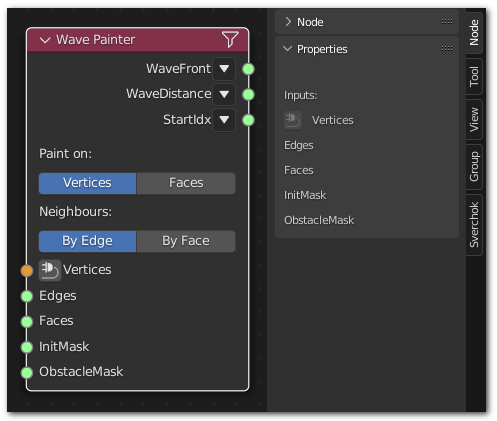
Functionality#
This node “paints” a wave pattern on either faces or vertices of the given mesh.
The pattern is drawn by the following algorithm (see Wikipedia):
First, the selected faces (or vertices) are marked with the number of 1.
Then the faces (vertices), that are neighbour to faces marked with 1, which were not marked yet, are marked with the number 2.
Faces (vertices), that are neighbour to faces marked with 2, which were not marked yet, are marked with the number 3.
This continues until all faces / vertices of the mesh are painted.
Some faces (vertices) of the mesh can be marked as obstacles, so that the wave can not pass through them.
Inputs#
This node has the following inputs:
Vertices. Mesh vertices. Mandatory input.
Edges. Mesh edges.
Faces. Mesh faces.
InitMask. Mask for faces (or vertices, depending on the painting mode), which should be considered as initially selected. This input is mandatory and must select at least one face / vertex.
ObstacleMask. Mask for faces / vertices, which should be marked as obstacles. If not connected, all faces / vertices are considered as passable.
Parameters#
This node has the following parameters:
Mode. Painting mode. The following modes are available:
Vertices. Paint on mesh vertices.
Faces. Paint on mesh faces.
Neighbour vertices. Visible only if Mode parameter is set to Vertices. This defines which vertices are considered to be neighbour. The available modes are:
By Edge. Vertices that share an edge are considered to be neighbour.
By Face. Vertices that share a face are considered to be neighbour.
The default value is By Edge.
Neighbour faces. Visible only if Mode parameter is set to Faces. This defines which faces are considered to be neighbour. The available modes are:
By Edge. Faces that share an edge are considered to be neighbour.
By Vertex. Faces that share a vertex are considered to be neighbour.
Outputs#
This node has the following outputs:
WaveFront. For each face (or vertex) of the mesh, this contains the number of steps which should be taken from initially selected faces (vertices), to take to this face (vertex), starting from 1 for initially selected faces. In other words, this is the number of the wave front. This output will contain 0 for obstacle faces / vertices and -1 if faces / vertices are unreachable from selected elements.
WaveDistance. For each face (or vertex) of the mesh, this contains the length of the shortest path from initially selected faces (vertices) to this face (vertex). The path is considered to be consisting of single steps from one face / vertex to one of it’s neighbours. The length of step between neighbour vertices is the Euclidean distance between such vertices. The length of step between neighbour faces is calculated as Euclidean distance between the centers of such faces. This input will contain 0 for initially selected faces as well as for obstacle faces and -1 for elements which are unreachable from selected ones.
StartIdx. For each face (or vertex) of the mesh, this contains the index of one of initially selected faces / vertices, which is the nearest from this face / vertex, in terms of the shortest path described above.
Examples of usage#
Start a wave from some small area on the hexagonal grid; mark some vertices as obstacles. Note how the wave can not pass through the obstacle and has to go the long way around:
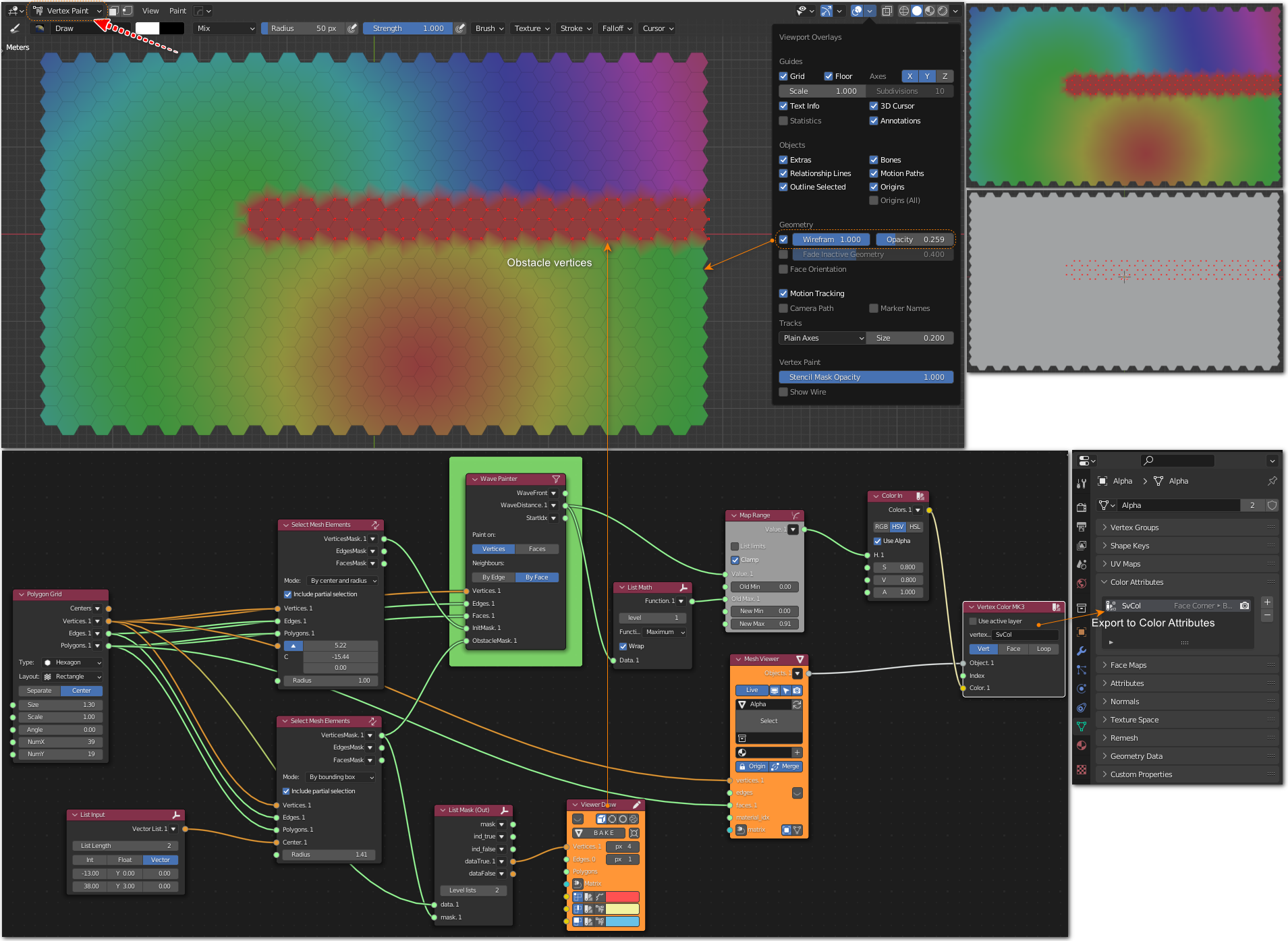
Generator->Generator Extended-> Polygon Grid
Analyzers-> Select Mesh Elements
Number-> Map Range
List->List Main-> List Math
List-> List Mask (Out)
Color-> Color In
Viz-> Mesh Viewer
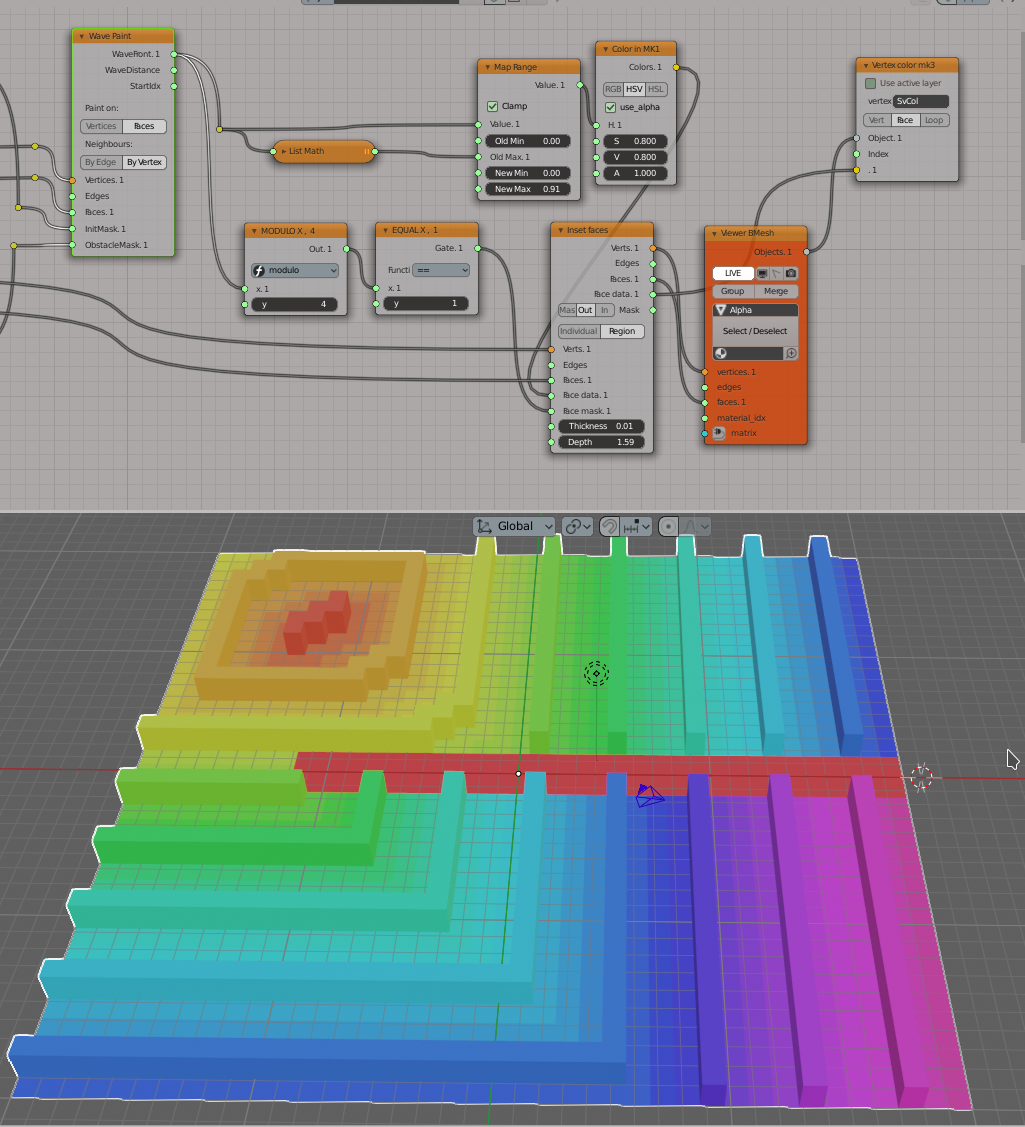
Similar setup with a rectangular grid; use wave front number to select faces to be extruded:
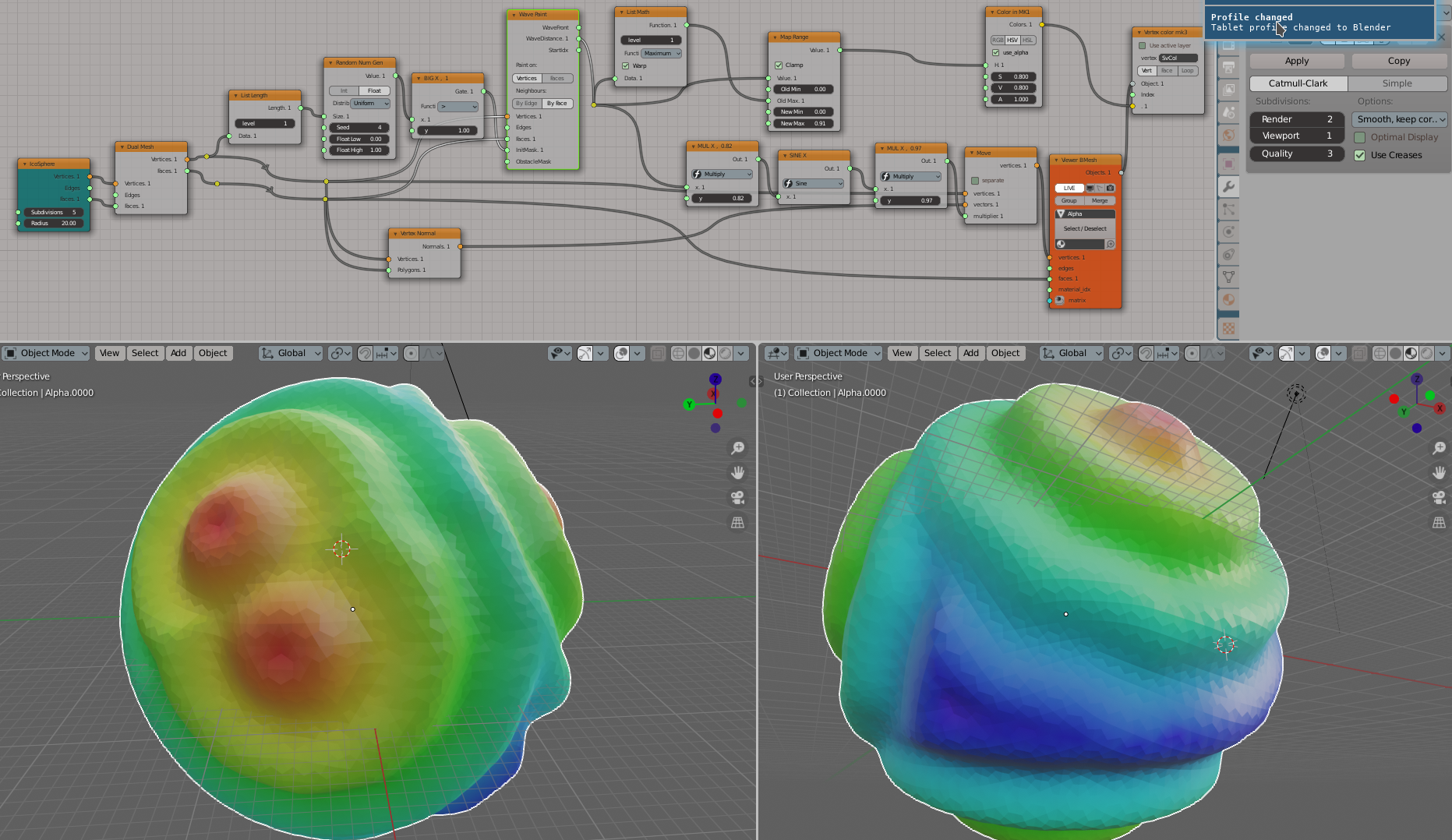
Select some random vertices on a dual mesh of the icosphere, and push the wave from them; use sine of wave distance to deform the mesh:
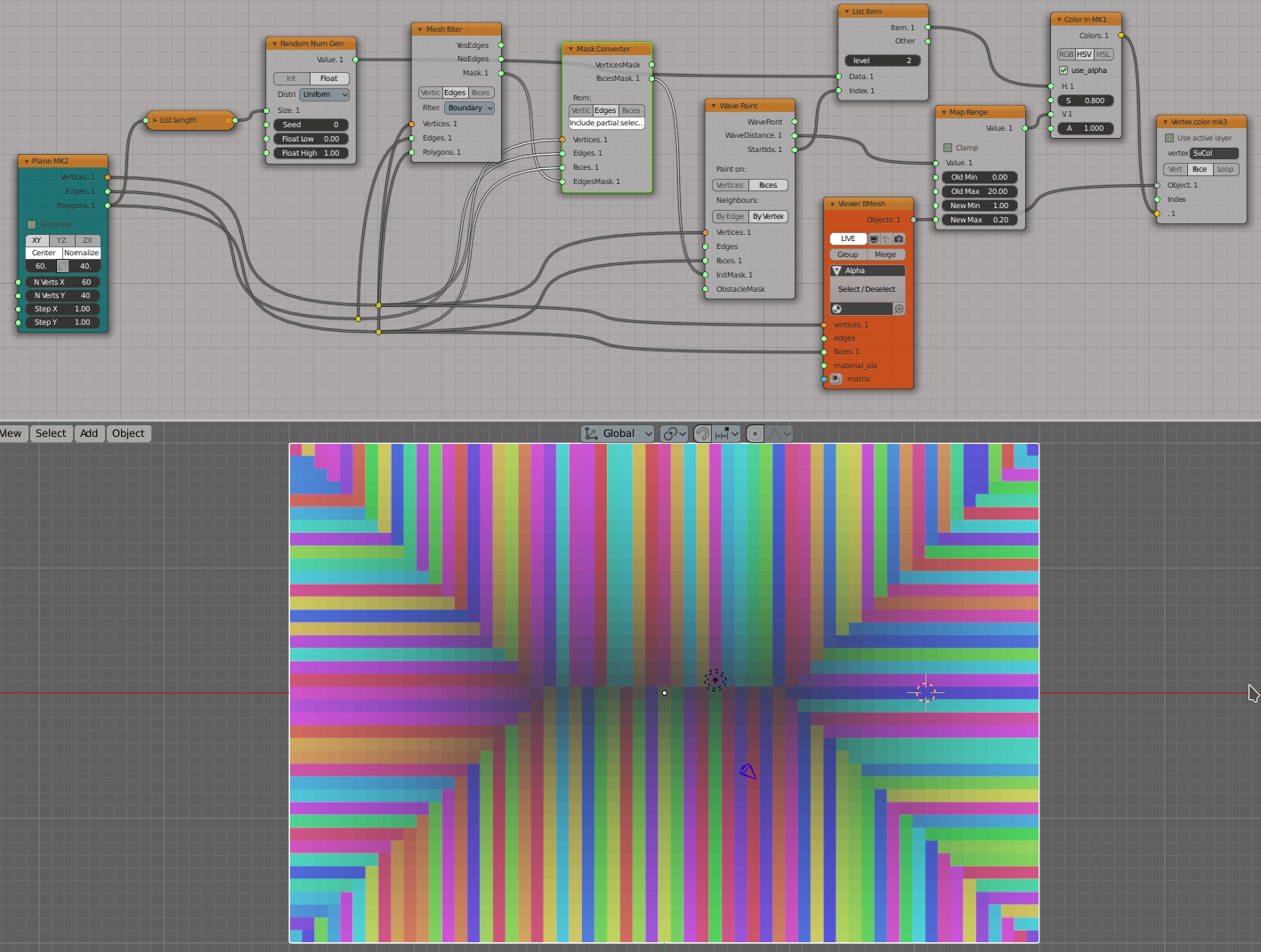
Paint the boundary faces of a rectangular grid with random colors; paint each other face with the color of the nearest boundary face; darken the color based on the distance from boundary. So here one single-colored stripe is actually the shortest path from some face to the boundary: