Map Scalar Field by Curve

https://github.com/nortikin/sverchok/assets/14288520/d894ad21-6ad0-4077-9509-8ffa7ac34c97

Functionality

This node generates a Vector Field object by applying a Curve object to Scalar Field object.

A Scalar Field is a function, which returns a number for each point in 3D space, i.e. S(v) : R^3 -> R. A Curve is a function, which returns a point in 3D space for each number in some domain, i.e. C(t) : R -> R^3. So, given a Scalar Field S and a Curve C, we can compose these two functions, to obtain a new function: V(v) = C(S(v)). This way we will have a function, which returns a 3D vector for each point in 3D space. Such function is called Vector Field.

If we have a Curve C, then we also have it’s tangent vector function T(t) : R -> R^3 and it’s normal vector function N(t) : R -> R^3. We can use these functions to compose them with a Scalar Field as well.

This node can be useful to construct vector (or scalar) fields of complex shape from a simple scalar field and some curve.

Inputs

This node has the following inputs:

  • Field. A Scalar Field to be used. This input is mandatory.

  • Curve. A Curve to be used. This input is mandatory.

Parameters

This node has the following parameter:

  • Curve usage. This defines what function of a curve will be used. The available options are:

    • Curve points. Radius-vectors of curve points will be used.

    • Curve tangents. Curve tangent vectors will be used.

    • Curve normals. Curve normal vectors will be used.

    The default value is Curve points.

Outputs

This node has the following output:

  • Field. The generated Vector Field object. You can use Decompose Vector Field node to deconstruct it into three scalar fields.

Example of usage

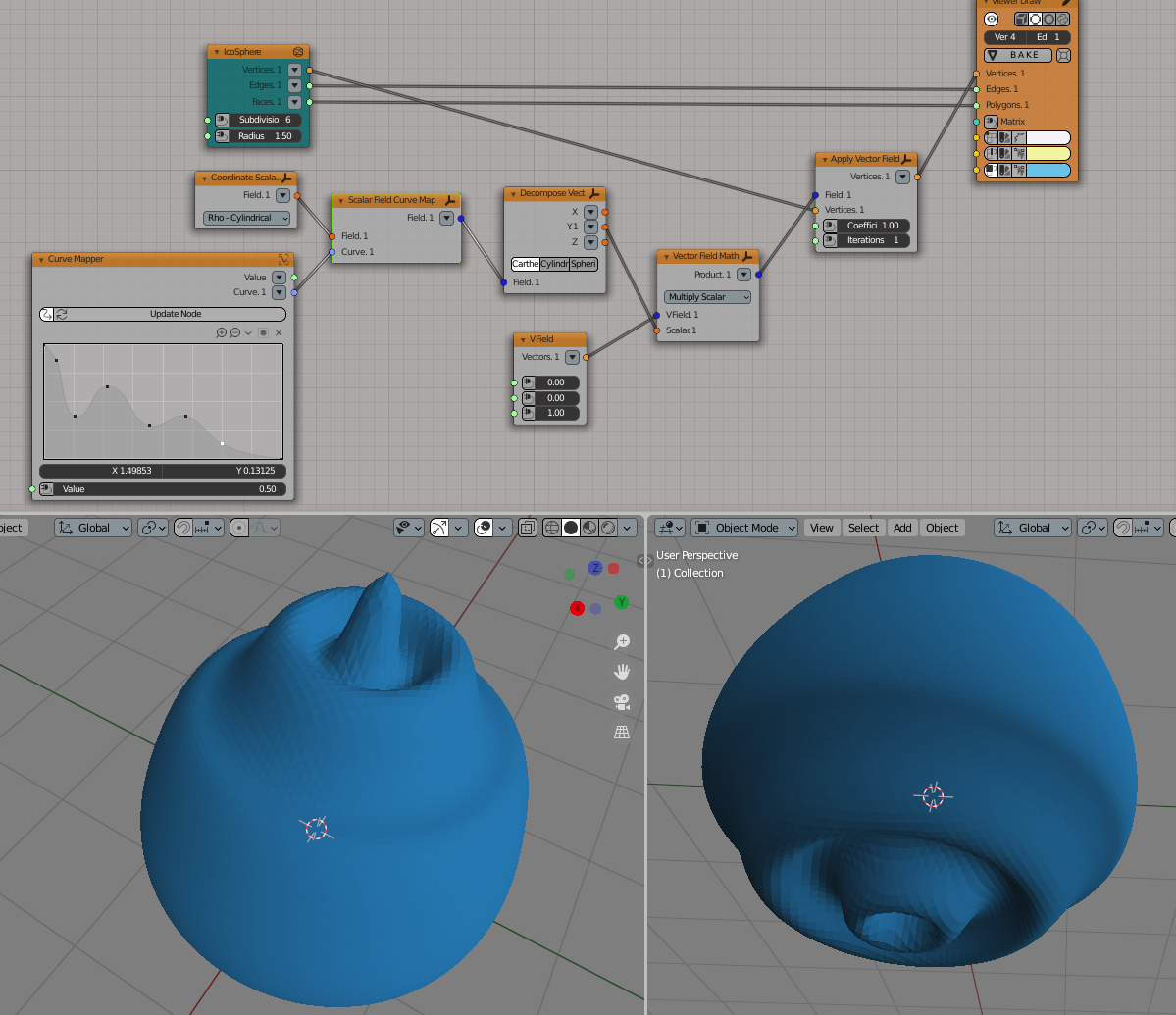
https://user-images.githubusercontent.com/284644/100201823-55371980-2f22-11eb-95de-faf66f46e4a8.png