Scalar Field Curvature

https://github.com/nortikin/sverchok/assets/14288520/5f91a473-ad6f-439d-94b4-1156af06002e

Functionality

This node calculates several types of information about implicitly defined surface curvature:

  • Principal curvature values

  • Gauss Curvature

  • Mean Curvature

You can refer to Wkikpedia for more detailed information about these terms.

If we have a scalar field defined by V = F(x,y,z), then at each point in space (x,y,z) it has a value of V; then through each point in space goes an iso-surface defined by F(x,y,z) = V. We can calculate curvature of that surface at that point. So, it appears that given one scalar field, we can define another one, defined by K(x,y,z) = Curvature(F(x,y,z) = V at (x,y,z)). We can simply evaluate that new scalar field at any point, for example at points of the surface F(x,y,z) = V itself; or we can do other strange things with this new scalar field…

The most clearly useful this will be in combination with “Marching Cubes” node from Sverchok-Extra addon, but may give interesting effects by itself.

Note that the calculation is done by numerical differentiation, so it may be not very precise in some cases.

Inputs

This node has the following input:

  • Field. The scalar field, for which the curvature is to be calculated. This input is mandatory.

Parameters

This node has the following parameter:

  • Step. Grid step for numericall differentiation. Bigger values give more smooth fields. The default value is 0.001.

Outputs

This node has the following outputs:

  • Gauss. Scalar field, values of which are Gaussian curvature values of iso-surfaces of the input scalar field.

  • Mean. Scalar field, values of which are mean curvature values of iso-surfaces of the input scalar field.

  • Curvature1. Scalar field, values of which are first principal curvature values of iso-surfaces of the input scalar field.

  • Curvature2. Scalar field, values of which are second principal curvature values of iso-surfaces of the input scalar field.

Examples of usage

Build some scalar field by “Attractor Field” node, measure it’s mean curvature and use that curvature values to color the vertices of a plane:

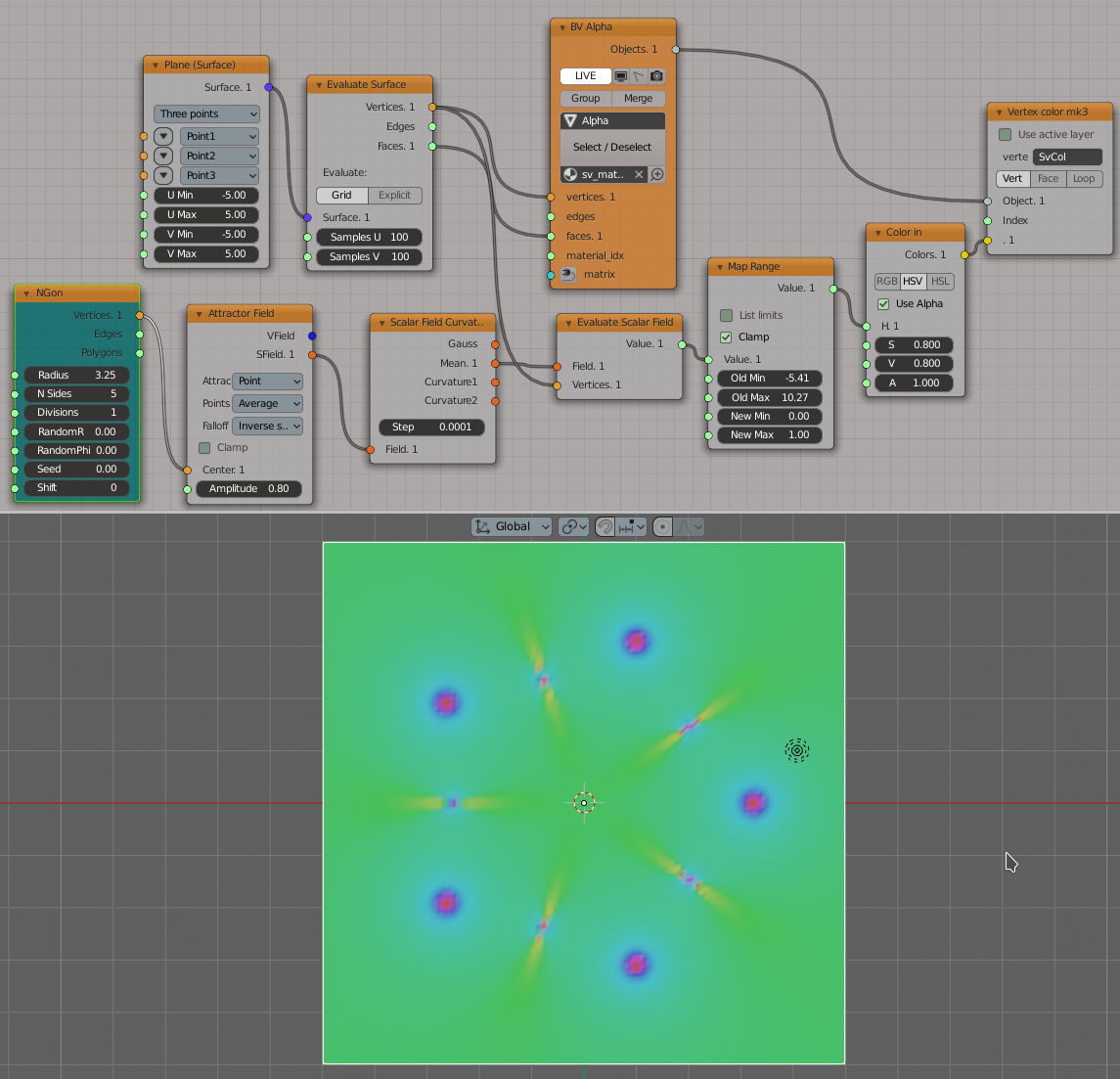
https://user-images.githubusercontent.com/284644/81438971-0e9cf000-9187-11ea-9d67-703b3550faf1.png

Generate an iso-surface of the same scalar field, and use it’s mean curvature values for coloring. Note: this example requires Sverchok-Extra addon for “Marching Cubes” node.

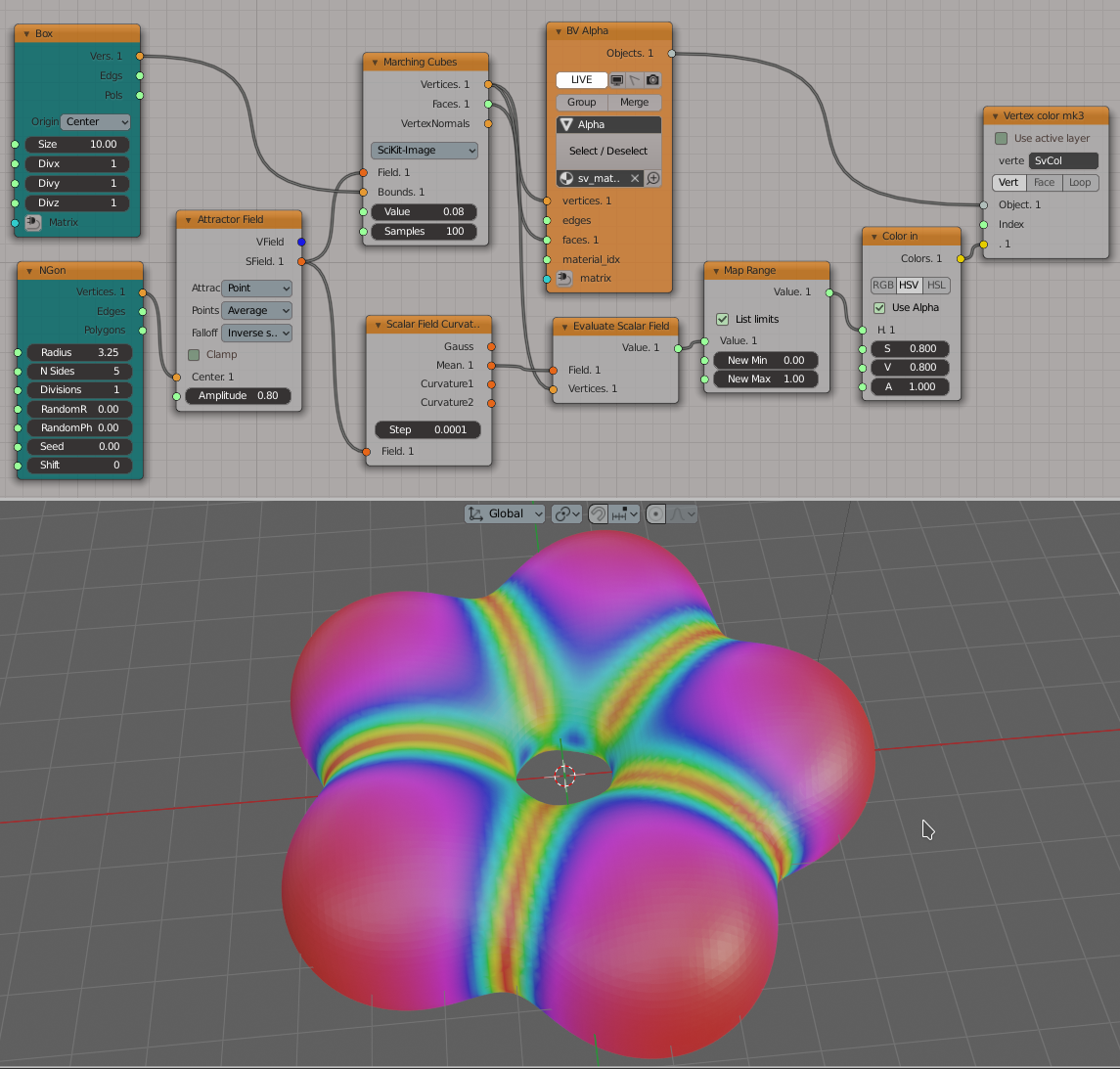
https://user-images.githubusercontent.com/284644/81438974-0fce1d00-9187-11ea-9583-1e8f4c6f8573.png