Catmull-Rom Spline#
Functionality#
This node generates a curve defined as Catmull-Rom spline through the specified set of points. This is a 3rd degree curve. The curve can be closed or not.
Catmull-Rom splines have the following advantages:
They are widely used in some areas like game design
They are quite fast to compute
They go exactly through specified points (i.e. they are interpolating)
They can be easily converted to Bezier segments or Nurbs curves.
In some implementations (see below), they allow to control the “degree of smoothness” with additional “tension” parameter.
But Catmull-Rom splines also have some disadvantages:
They have only C1 continuity, i.e. first derivative is continuous, but second is not.
As consequence, their curvature can change very fast — they can be “very curvy” at one points and “almost straight” in others. But this property can be useful in some applications, when you want the spline to go almost by straight lines, just rounding the corners a bit.
This node supports two variants of Catmull-Rom spline:
Non-uniform spline (refer to Wikipedia). In this implementation, each spline segment (between two successive points) is assigned with different span of T parameter, which is calculated based on distance between points (several metrics are supported). This has the effect of the curve being more “curvy” in places where control points are far from one another, and more flat where control points are near. This usually gives the feeling of curve being more “natural”.
Generator->Generatots Extended-> Spiral
Viz-> Viewer Draw
Viz-> Viewer Draw Curve
Uniform spline. In this implementation, each spline segment is assigned with equal span of T parameter. As effect, it is possible that the curve will be unexpectedly more “curvy” when successive control points are near one another. But this implementation has an option to control the degree of curve “smoothness” by additional “tension” parameter. It is also possible to specify tension value for each curve segment.
Generator->Generatots Extended-> Spiral
Viz-> Viewer Draw
Viz-> Viewer Draw Curve
Inputs#
This node has the following inputs:
Vertices. The points through which the curve should go. This input is mandatory. At least two points are required to build the spline.
Tension. This input is available only when Spline Type parameter is set to Uniform (with tension). Specifies the tension value of the spline. Lesser values of tension mean that the curve will go segments of straight lines between points. It is possible to provide a separate value for each segment of the curve (i.e. for each pair of successive points). The default value is 1.0.
Parameters#
This node has the following parameters:
Cyclic. Defines whether the curve should be cyclic (closed). Unchecked by default.
Spline Type. Allows to select one of Catmull-Rom spline implementations (see descriptions above). The available options are Non-uniform and Uniform (with tension). The default option is Non-uniform.
Metric. This parameter is available only if Spline Type is set to Non-uniform. Defines the metric used to assign T parameter spans to each segment of the curve. The available values are:
Manhattan
Euclidean
Points (just number of points from the beginning)
Chebyshev
Centripetal (square root of Euclidean distance)
X, Y, Z axis - use distance along one of coordinate axis, ignore others.
Most used options are Euclidean (in this case the spline is called chordal Catmull-Rom spline), Centripetal (centripetal Catmull-Rom spline), and Points (this makes a uniform spline with tension set to 1). The default option is Euclidean.
Outputs#
This node has the following output:
Curve. The generated curve object.
Examples of Usage#
Simplest example:
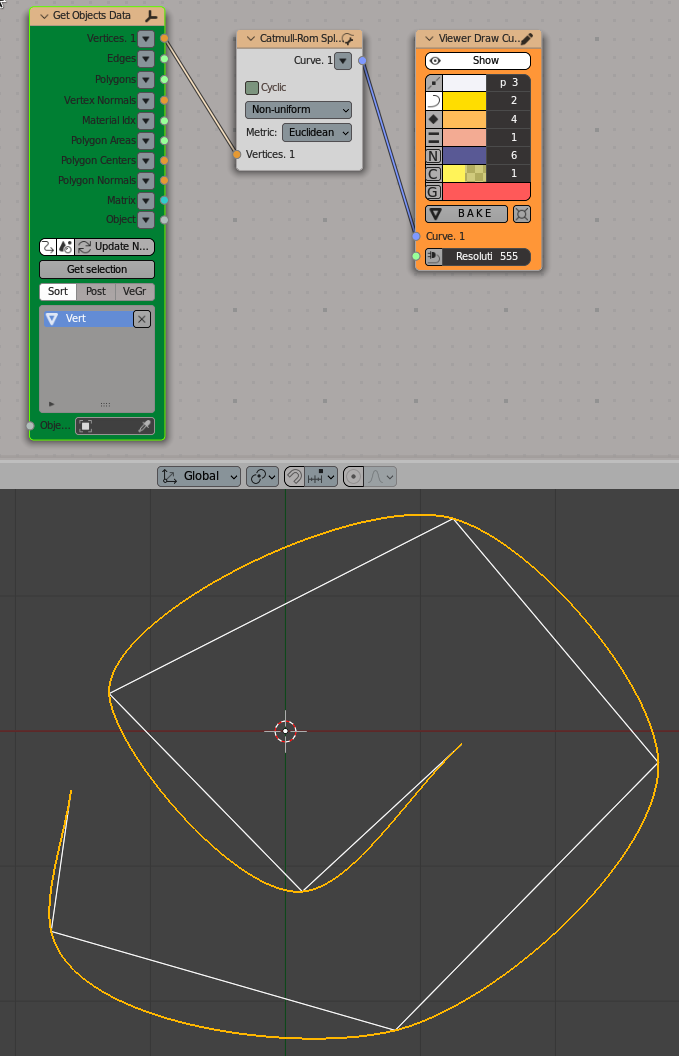
Viz-> Viewer Draw Curve
Scene-> Get Objects Data
Uniform (yellow) vs non-uniform (green) spline:
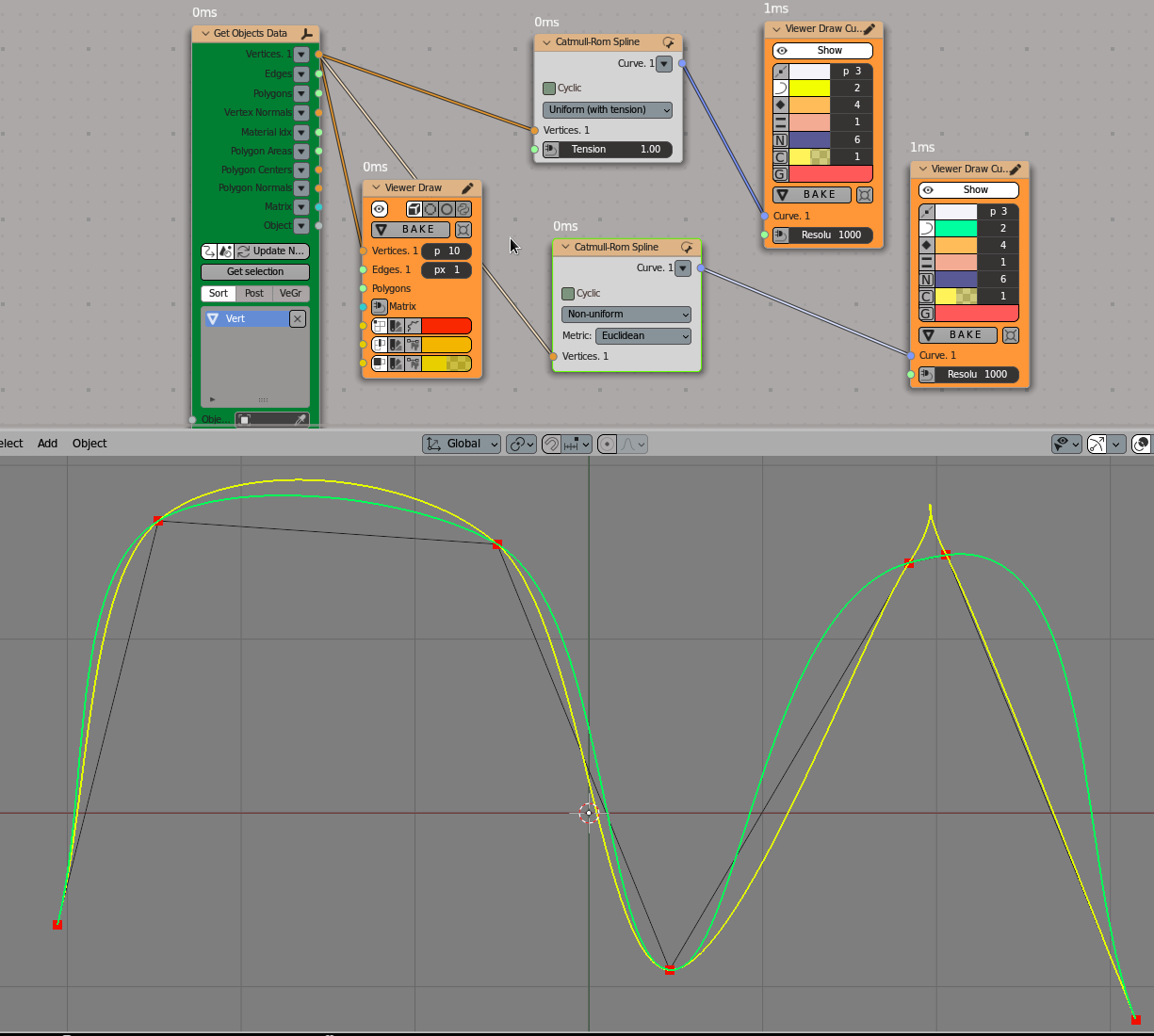
Viz-> Viewer Draw
Viz-> Viewer Draw Curve
Scene-> Get Objects Data
Non-uniform splines with Euclidean metric (yellow) and with centripetal metric (green):
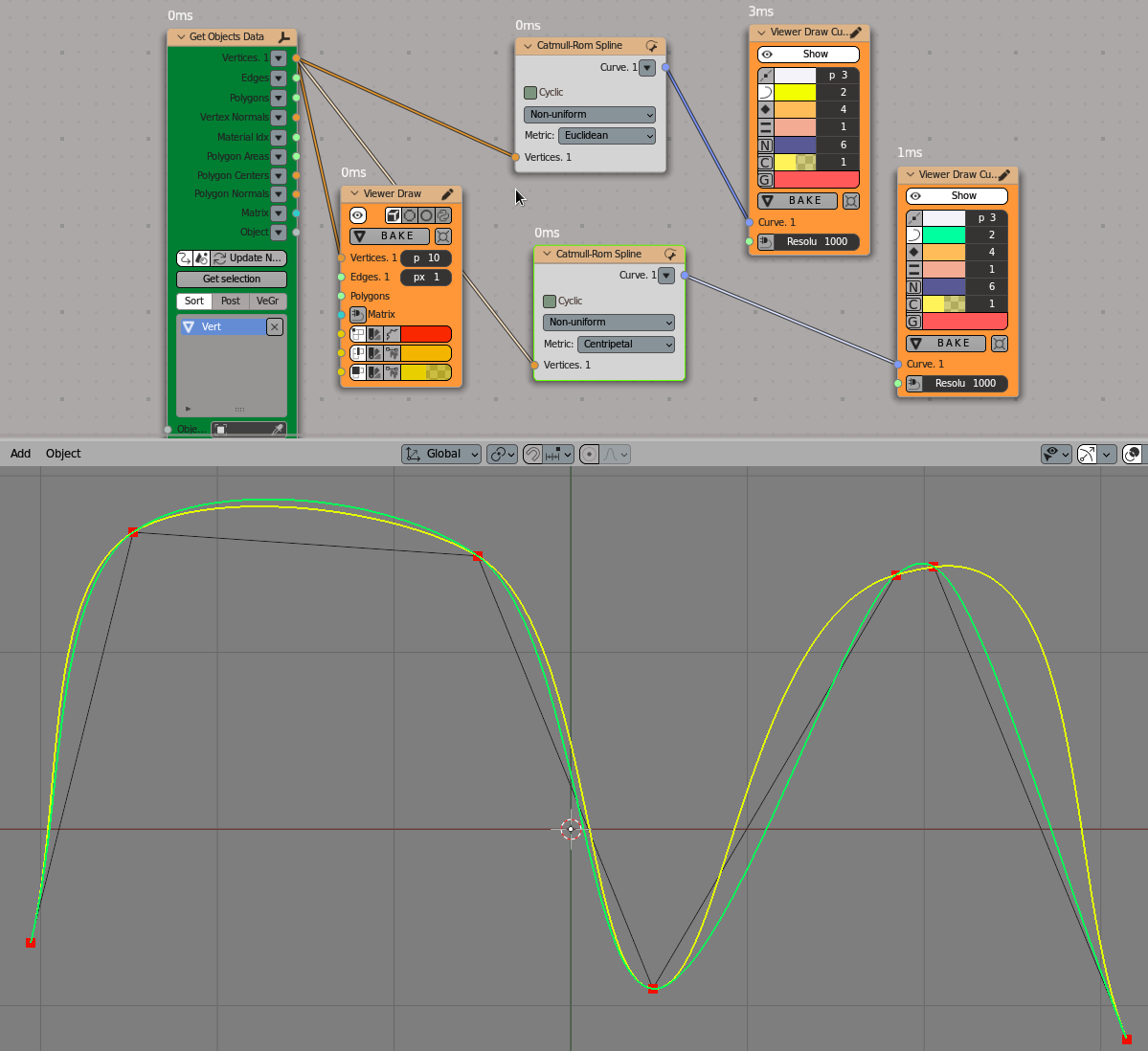
Viz-> Viewer Draw
Viz-> Viewer Draw Curve
Scene-> Get Objects Data
Non-uniform (Euclidean) Catmull-Rom spline (yellow) vs Cubic spline (blue):
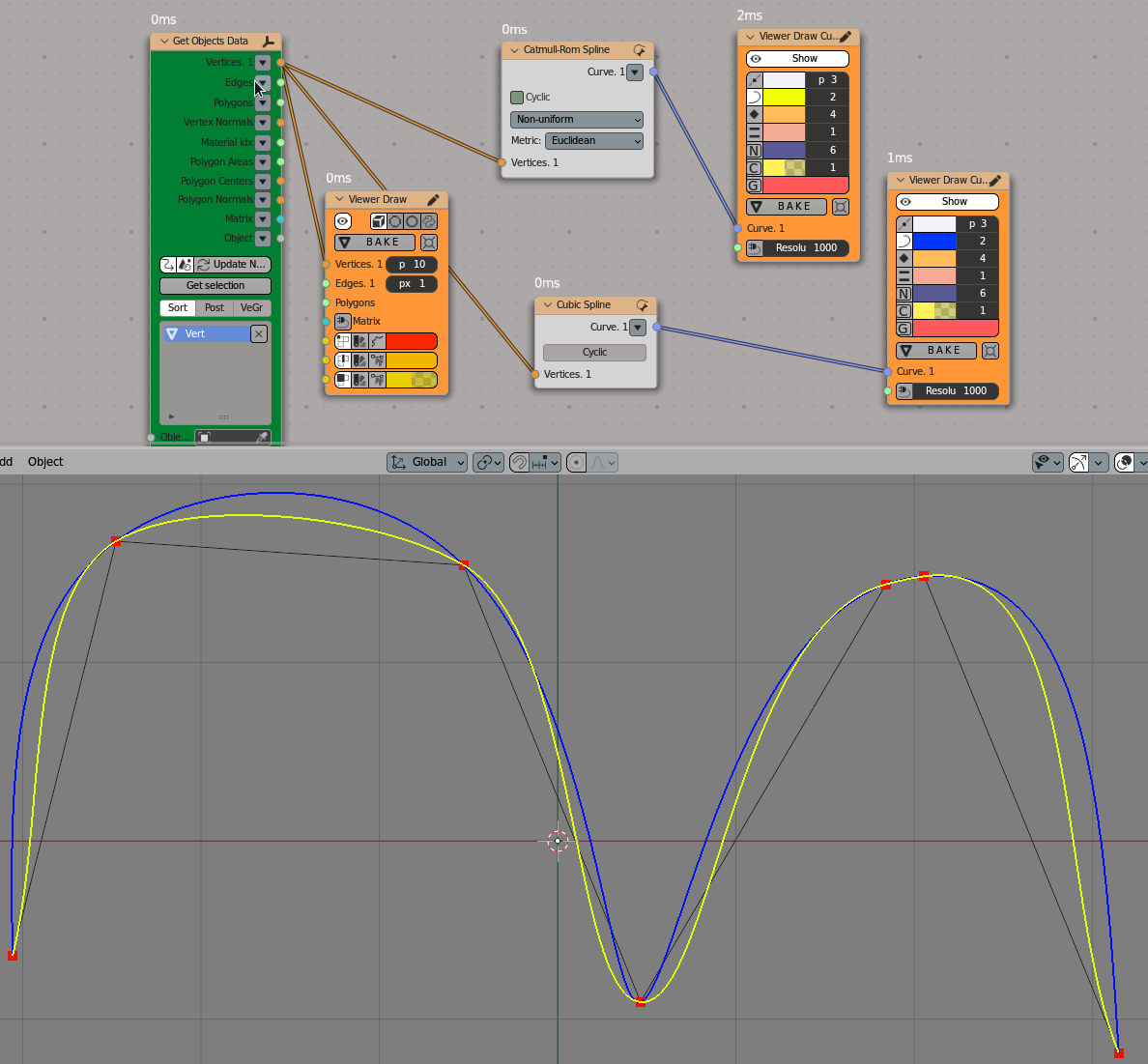
Viz-> Viewer Draw
Viz-> Viewer Draw Curve
Scene-> Get Objects Data
Uniform splines with different tension values: from 0.2 (almost black lines) to 2.0 (white line):
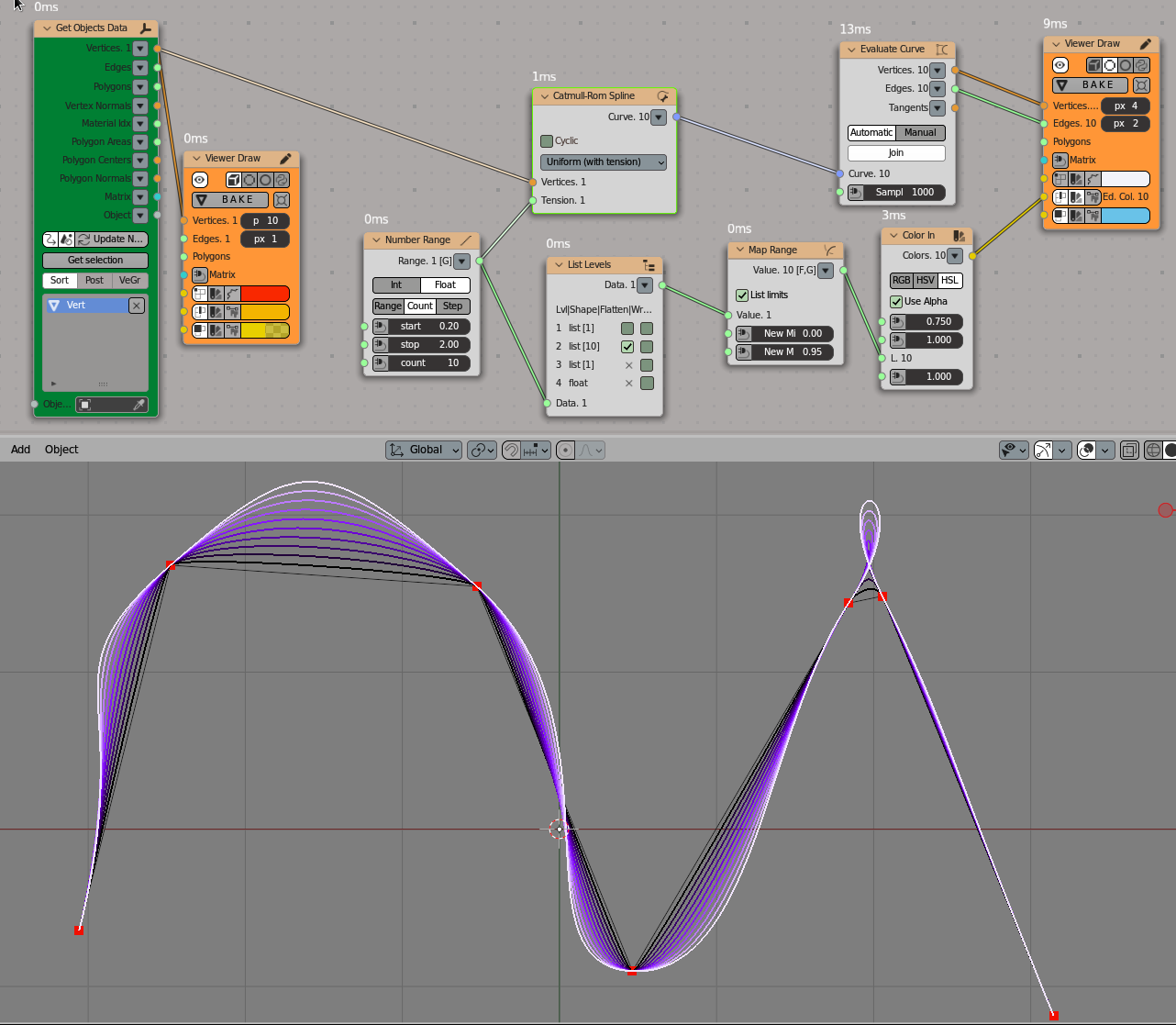
Number-> Number Range
Number-> Map Range
Curves-> Evaluate Curve
List->List Struct-> List Levels
Color-> Color In
Viz-> Viewer Draw
Scene-> Get Objects Data
Here the curvature comb is used to illustrate that the curvature of Catmull-Rom splines can change very fast and sudden:
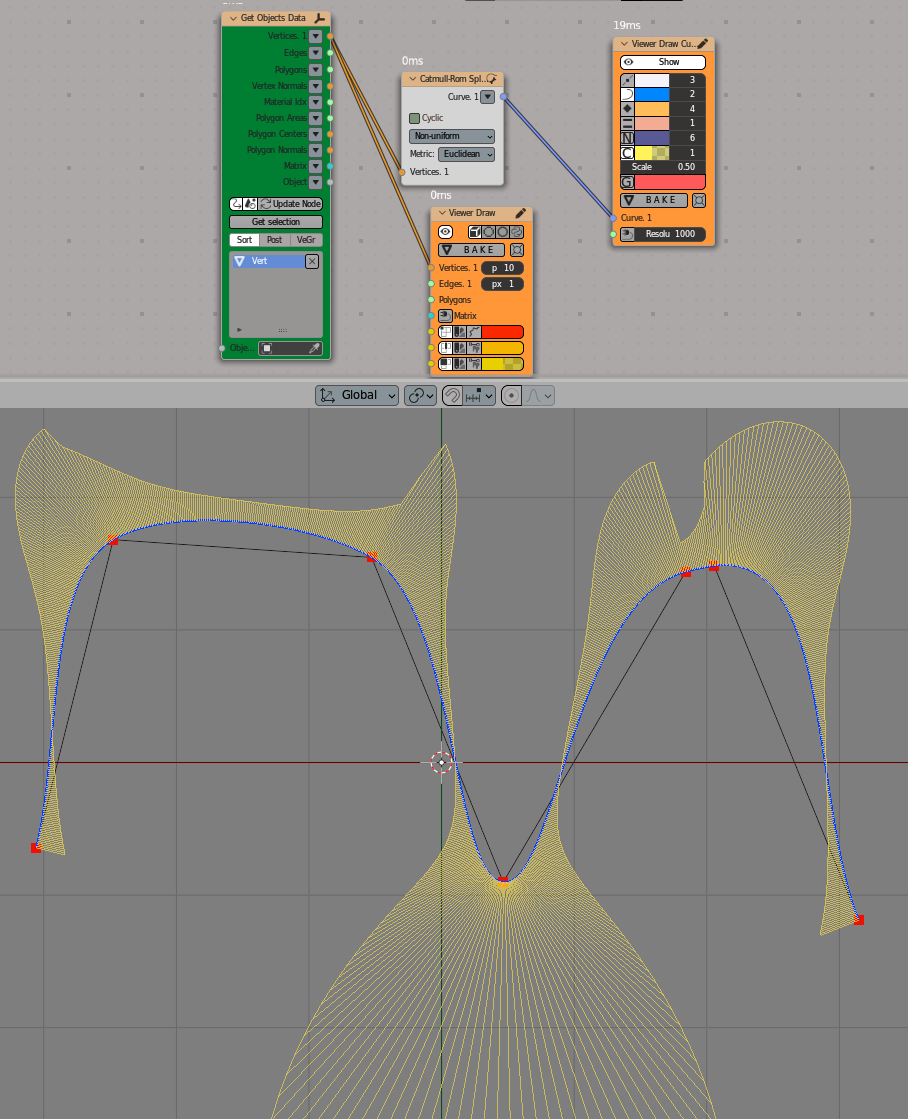
Viz-> Viewer Draw
Viz-> Viewer Draw Curve
Scene-> Get Objects Data