NURBS Surface from Curves Net

Functionality

Given a net of intersecting curves, this node generates a surface which passes through all given curves.

A net of curves is two sets of curves, one set along one direction and one set along another. One set of curves is called “U-curves” (curves along U direction) and another set of curves is called “V-curves” (curves along V direction).

Apart of curves grid, this node requires intersection points of curves provided explicitly. Intersection points can be calculated by use of “Intersect NURBS curves” node. Note: that node uses numeric algorithms to calculate intersections, so it can fail to find intersections, or give imprecise results. So, if you have intersection points in advance, it’s better to use them.

This node generates a NURBS surface from NURBS curves according to algorithm known as “Gordon Surface”.

“Gordon Surface” algorithm has a number of restrictions:

• All input curves must be NURBS or NURBS-like. More specifically, only non-rational curves are supported - i.e., without weights (or all weights equal).

• All U-curves must have “the same” direction; all V-curves must also have “the same” direction.

• There must be N curves along one direction, and M curves along another direction, which must exactly intersect at N x M points.

• Intersection points must be located evenly in parameter spaces of curves. For example, V-Curve C_v must intersect all U-curves C_u at the same value of U parameter. In other words, intersection points must be located so that given curves would represent iso-curves of some surface, along U and V directions correspondingly.

• U-curves must be ordered along direction of V-curves, and vice versa. For example, if U-curve C_u1 intersects V-curve C_v at v = v1, and another U-curve C_u2 intersects the same V-curve C_v at v = v2, and v1 < v2, then in input curves list, C_u1 must be provided before C_u2.

If some of these requirements are not met exactly, then the resulting surface will pass through the curves only approximately.

If intersections of your curves are located arbitrarily in parameter spaces of curves, the node can try to reparametrize curves in order to make intersections located “even” in parameter spaces. Note that reparametrization algorithm is somewhat rude, so it can produce unwanted additional control points, and/or create “bad” parametrization of resulting surface. In some cases, it is possible to get a better parametrization by manually removing excessive knots.

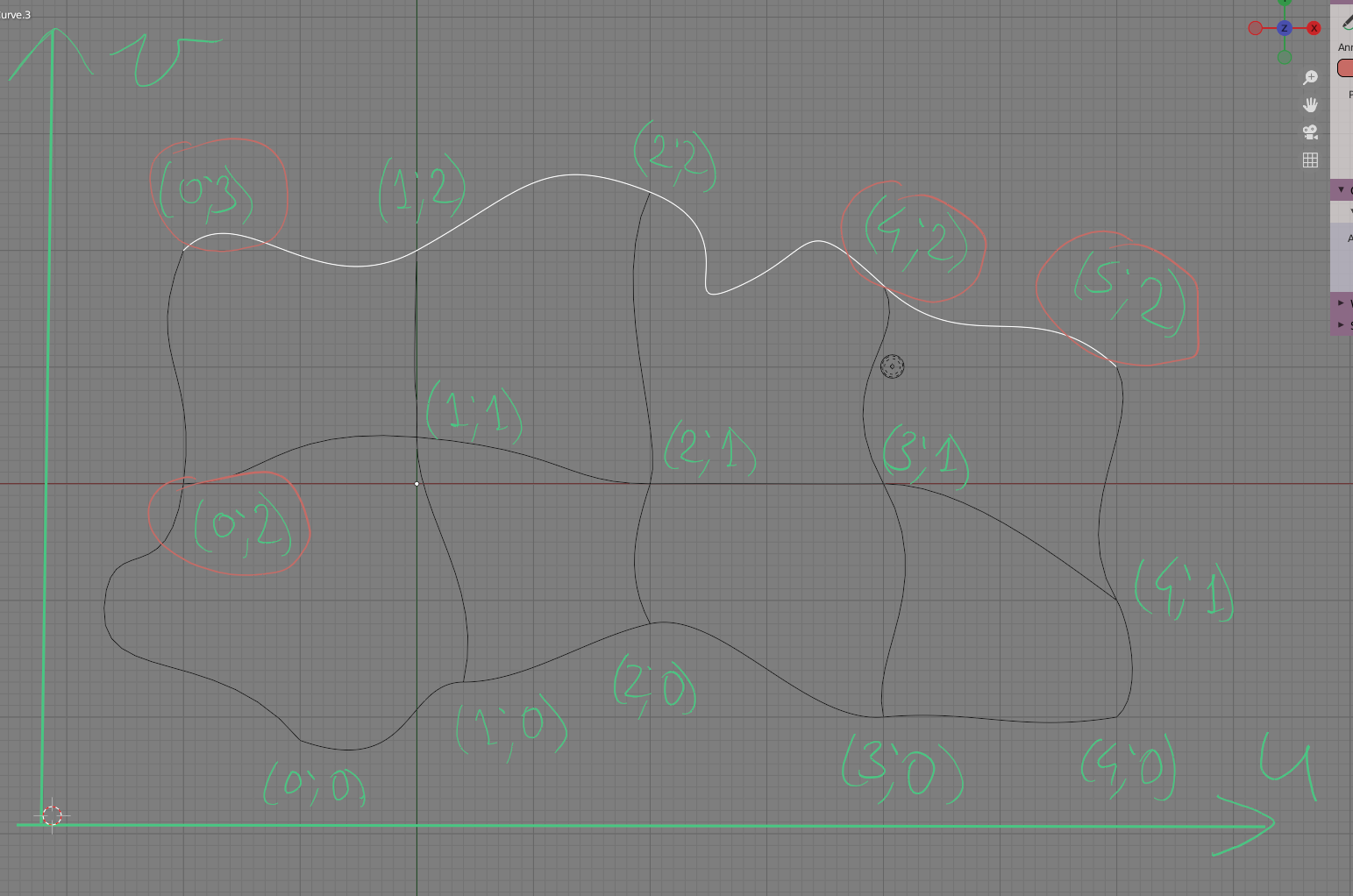
To clear the issue of intersections location in parameter space, let’s draw some pictures.

Good parametrization: (first number is parameter of U-curve at the intersection point, the second number is parameter of V-curve at the intersection point):

Note that when you move from left to right, U value is changing by the same amount at all U-curves. And when you move from bottom to top, V-value is changing by the same amount at all V-curves.

“Bad” parametrization:

Inputs

This node has the following inputs:

• CurvesU. Set of curves along U direction. This input is mandatory. At least two U-curves is required to build a proper surface.

• CurvesV. Set of curves along V direction. This input is mandatory. At least two V-curves is required to build a proper surface.

• T1. This input is available and mandatory when Explicit T values parameter is checked. For each U-curve, this input should contain a list of T parameter values, at which this curve intersects V-curves.

• T2. This input is available and mandatory when Explicit T values parameter is checked. For each V-curve, this input should contain a list of T parameter values, at which this curve intersects U-curves.

• Intersections. Intersection points of curves. For each U-curve, this input must contain a list of points (in 3D space), where this curve intersects V-curves. This input is mandatory.

Parameters

This node has the following parameters:

• Explicit T values. If checked, the node expects the user to provide T parameter values of curve intersections in T1 and T2 inputs. In this case, the node will try to automatically reparametrize input curves in order to make intersection points located “evenly” in curve’s parameter space (see illustrations above). If not checked, the node will calculate T values of intersections according to Metric parameter. Unchecked by default.

• Metric. This node is available in the N panel only, and only when Explicit T values parameter is not checked. This defines the metric, which the node should use to calculate T values of curve intersections, when they are not provided by user. The available options are:

  • Manhattan

  • Euclidean

  • Points (just number of points from the beginning)

  • Chebyshev

  • Centripetal (square root of Euclidean distance).

  The default option is Points. In most cases, this option gives the best results.

• Knotvector accuracy. This parameter is available in the N panel only. Number of decimal digits (after decimal point), to which the node should round values in resulting surface’s knot vectors. More decimal digits will give more exact results, but can produce a number of knots / control points located very close to each other, most of them being just an artefact of floating-point precision issues. The default value is 4.

Outputs

This node has the following output:

• Surface. The resulting NURBS surface.

Examples of usage

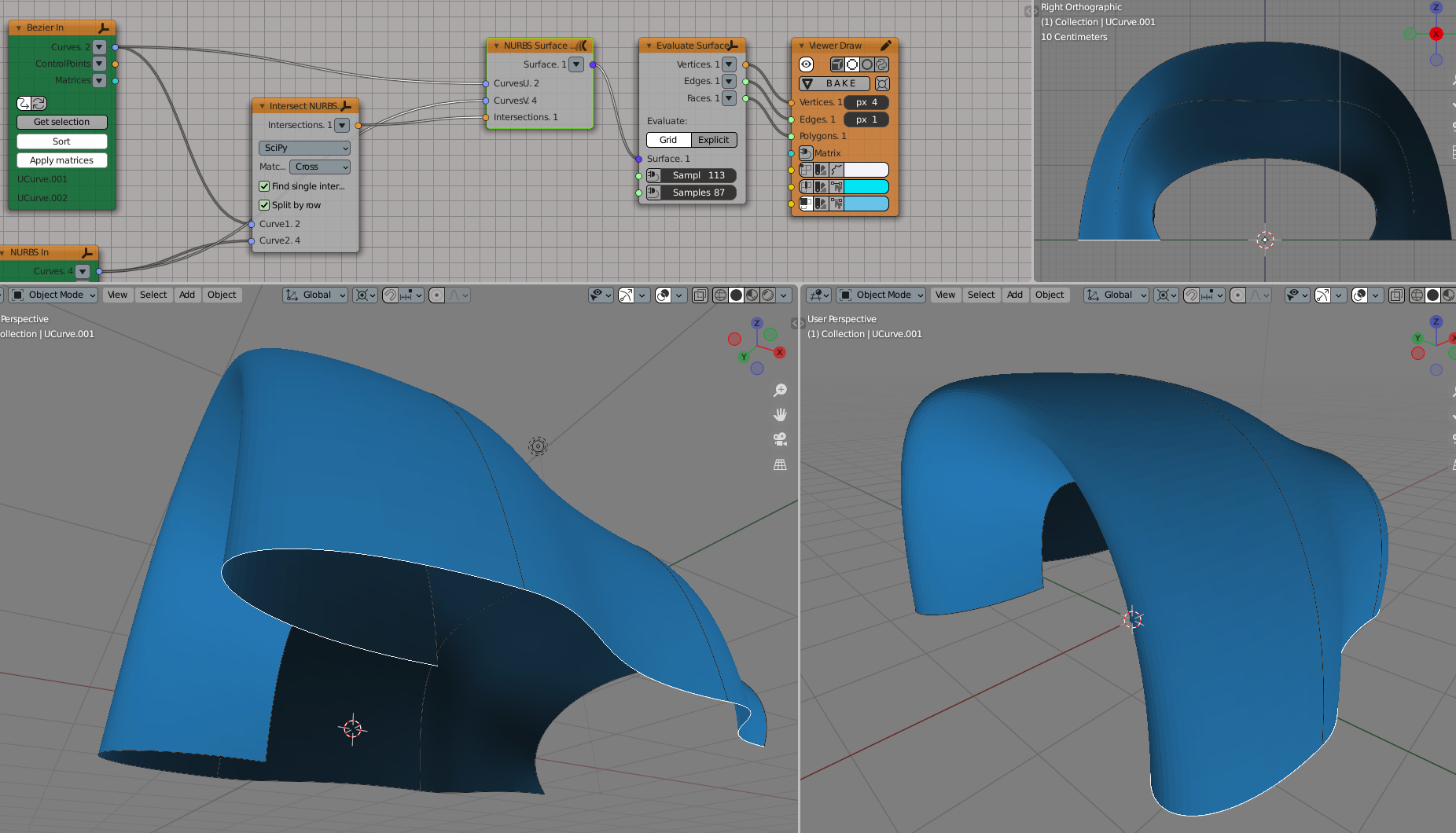
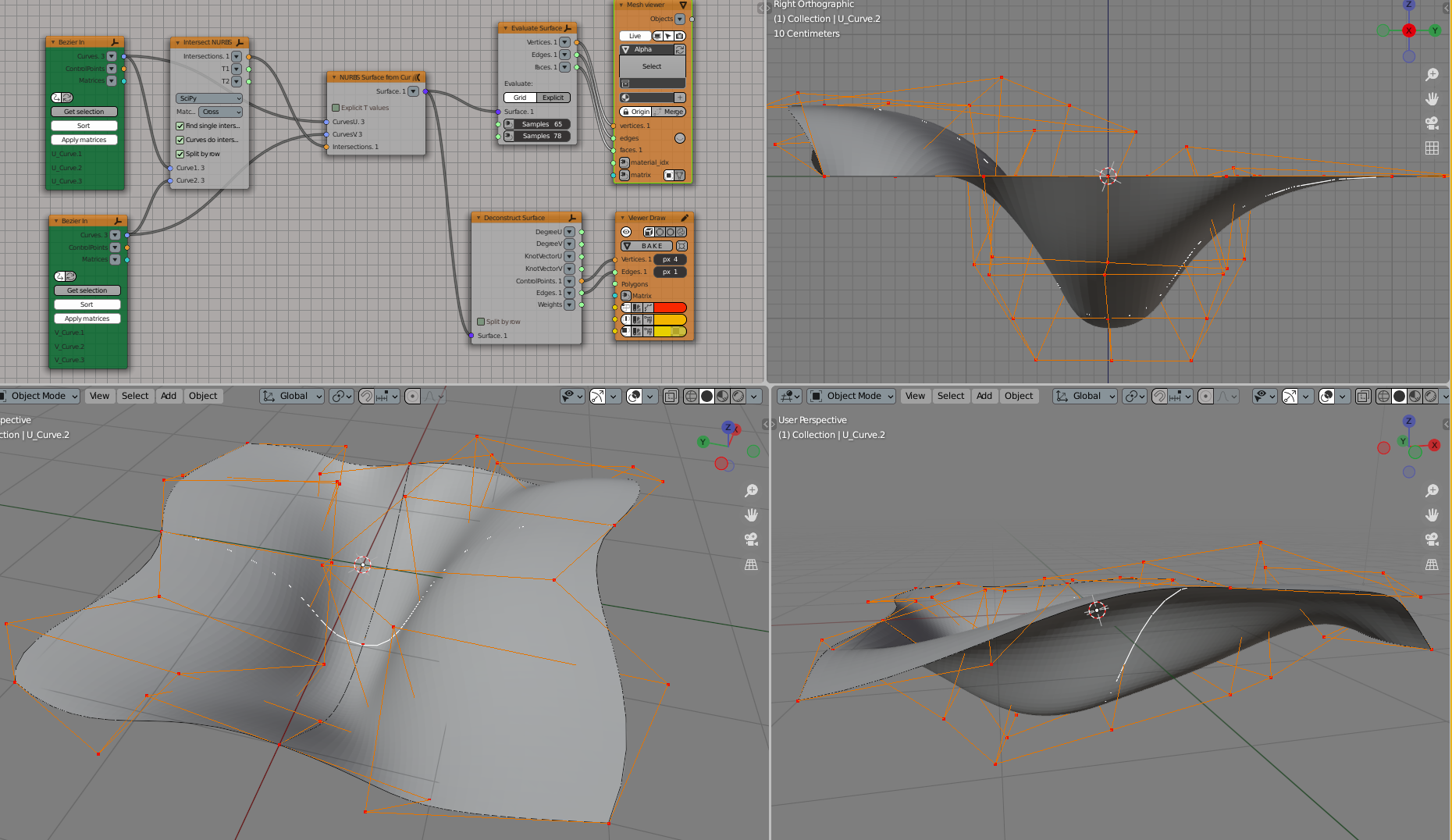
There are some other examples at github’s PR page: https://github.com/nortikin/sverchok/pull/4183